Geometrically unfitted finite element methods

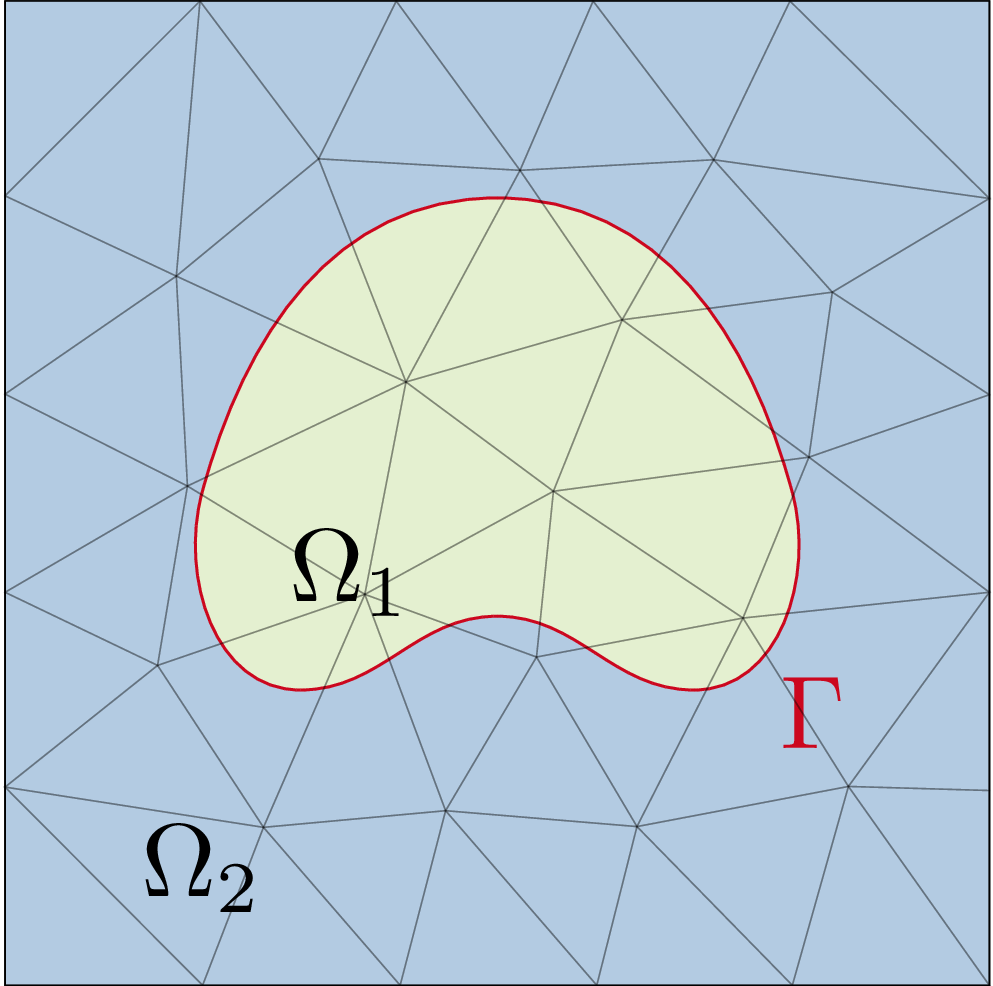
In physics, biology, chemistry and engineering many applications of simulation science involve complex and evolving geometrical shapes. In many important problems these geometrical shapes exhibit topology changes or strong deformation which makes the numerical treatment very challenging. The highly accurate and efficient numerical solution of PDEs on these evolving domains is a challenging task. In the past two decades research on this topic has been started. Especially methods using a geometry description which is separated from the computational mesh and in turn provide a more flexible handling of the geometry compared to traditional conforming mesh descriptions have become very popular in recent years. Although big progress has been made, numerical methods which are flexible with respect to the geometrical configuration, robust and high order accurate at the same time are missing.

We are investigating finite element methods which are suitable for an integration with a separated geometry description and have provable higher order error bounds. This entails several issues:

1. First, a higher order representation of the geometry is necessary. For that most often an implicit description with an indicator function is used. While the geometry description typically works well, the practical usability of the description poses a problem. For suitable finite element formulations integrals on cells which are cut are required. Due to the fact that these domains are only described implicitly, an accurate numerical integration is difficult. While for a second order accuracy robust and established methods exist, the extension to higher order accuracy requires new approaches in the discretization.

2. Another important problem consists of the handling of the geometry evolution. With an implicit geometry description the evolution of the geometry can be handled without adapting the computational mesh, but new challenges arise with respect to the time discretization for problems on evolving domains.