Research

In the working group we are interested in the numerical solution of different classes of PDE problems, mostly based on finite element methods. Challenges that need to be tackled may be different for different problems. Sometimes a reliable solution can be obtained, but efficiency is a major problem. Sometimes the stable solution is not yet clear and sometimes structure and robustness properties are not satisfactory. Main topics are structure preserving discretizations for flow problems, efficient realization of modern discretization methods and flexible discretization for PDEs on moving domains, so-called unfitted finite element methods.

Major research topics

Structure preserving discretizations for flow problems

The divergence-constraint in incompressible Navier-Stokes equations gives rise to a very special structure and can elegantly be respected by the use of \(H(\operatorname{div})\)-conforming finite element methods. The application and analysis of such discretizations is one of the major topics of our working group. More details are given here.

Hybrid Discontinuous Galerkin methods

Hybrid Discontinuous Galerkin (HDG) methods are used to compensate for the costs of Discontinuous Galerkin (DG) methods and play an important rule to render some classes of discretizations efficiently computable when solving linear systems is involved. More details are given here.

Geometrically unfitted finite element methods

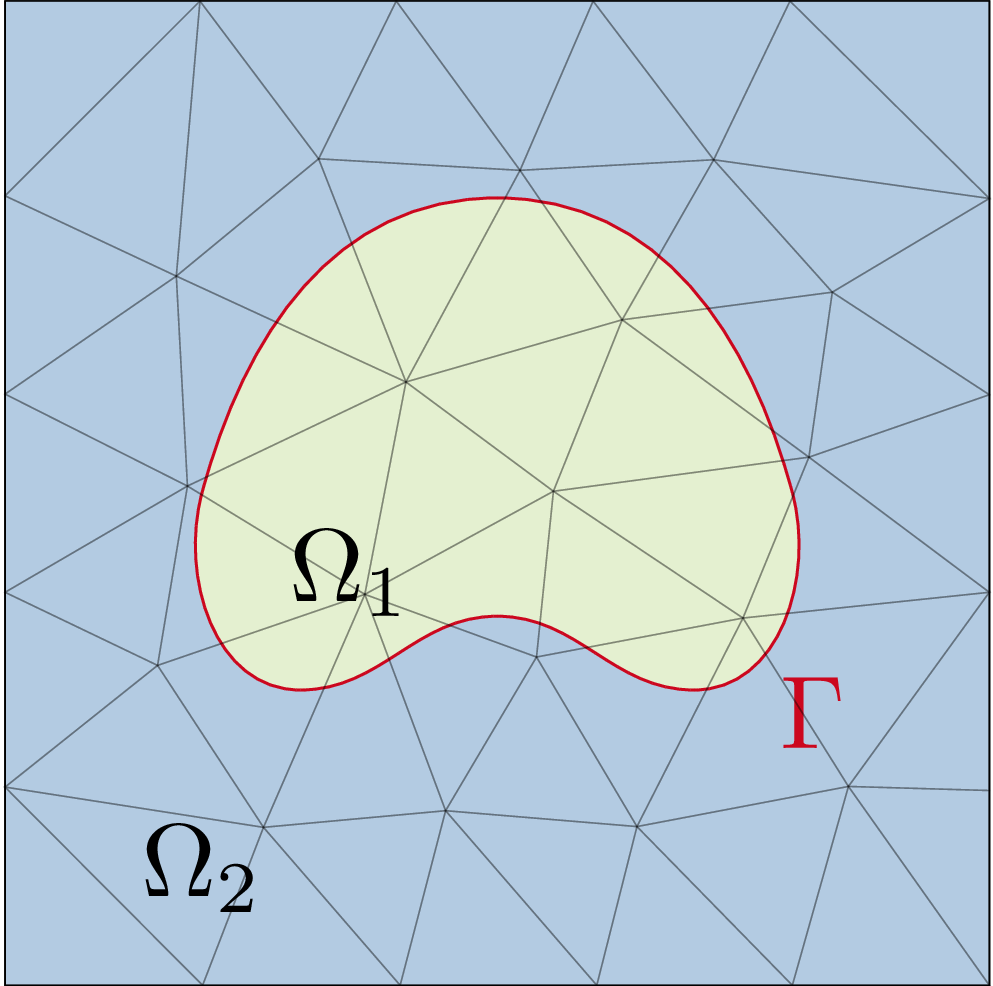
The development and analysis of numerical methods which are flexible with respect to the (possibly time-dependent) geometrical configuration of a PDE, robust and high order accurate at the same time are the second major research topic of our working group. Technologies like level set methods, unfitted finite element methods and space-time formulations are combined and enhanced to obtain reliable numerical methods. More details are given here.

Running research projects

Unfitted space-time FEM

We discretize PDEs on moving domains using unfitted finite elements in a space-time formulation. To handle the geometry with higher order accuracy we apply a space-time version of an isoparametric mapping and prove higher order a priori error bounds.

Embedded Trefftz DG methods

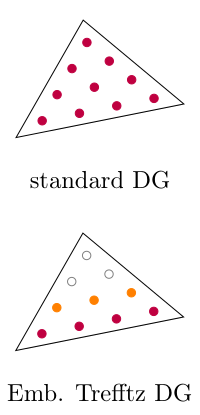
Discontinuous Galerkin (DG) methods are widely used to discretize PDEs. One drawback of DG methods is the increased number of degrees of freedom (ndof) compared to CG methods. We introduce Embedded Trefftz DG methods which are (more than) an alternative to HDG methods. Embedded Trefftz DG methods allow for an efficient and flexible implementation of Trefftz DG methods and the introduction of weak Trefftz DG spaces. Both together allow to apply Trefftz DG methods for a large range of PDE problems.

Unfitted BDF-FEM for moving domains

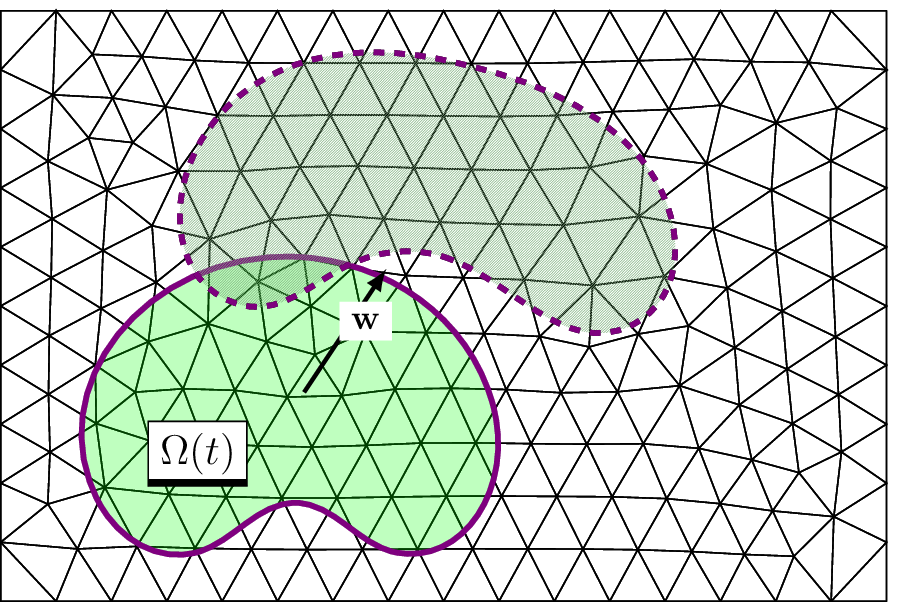
We discretize PDEs on moving domains using unfitted finite elements combined with BDF time stepping. This is made possible using discrete extensions via ghost penalty stabilizations. To handle the geometry with higher order accuracy we apply isoparametric mappings and introduce an efficient projection between differently deformed meshes.

Numerical methods for Helioseismology

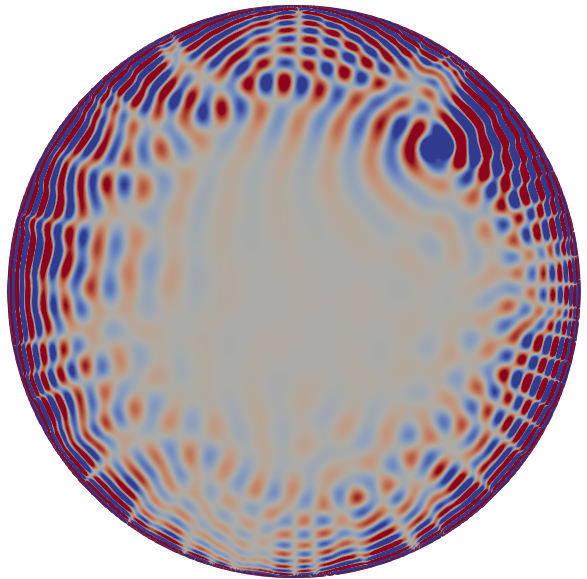
We develop numerical methods to accurately and efficiently discretize the equations of solar and stellar oscillations. Our research is driven by the field of helioseismology, which seeks to understand the Sun's internal structure through its oscillations.

Learned infinite elements

We investigate transparent boundary conditions for time-harmonic wave equations in stratified media, e.g. stemming from helioseismology and construct special infinite elements which are ‘learned’ from the background medium in order to optimize approximation of the Dirichlet-to-Neumann operator.