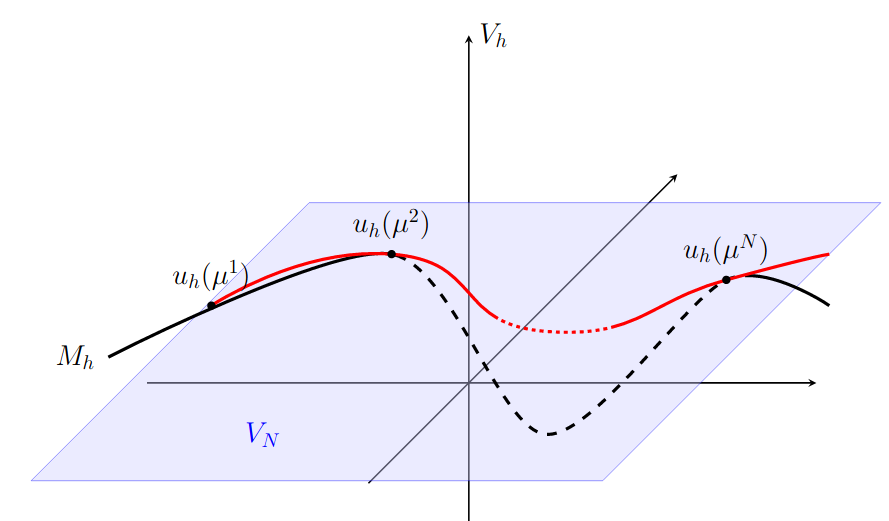
[HLP25]
|
Fabian Heimann, Christoph Lehrenfeld, and Janosch Preuß.
Discretization error analysis of a high order unfitted space-time
method for moving domain problems.
IMA Journal on Numerical Analysis, pages 1--41, 12 2025.
[ bib |
DOI |
arXiv |
http |
.pdf ]
Keywords: moving domains, unfitted FEM, isoparametric FEM, space–time, higher order
|
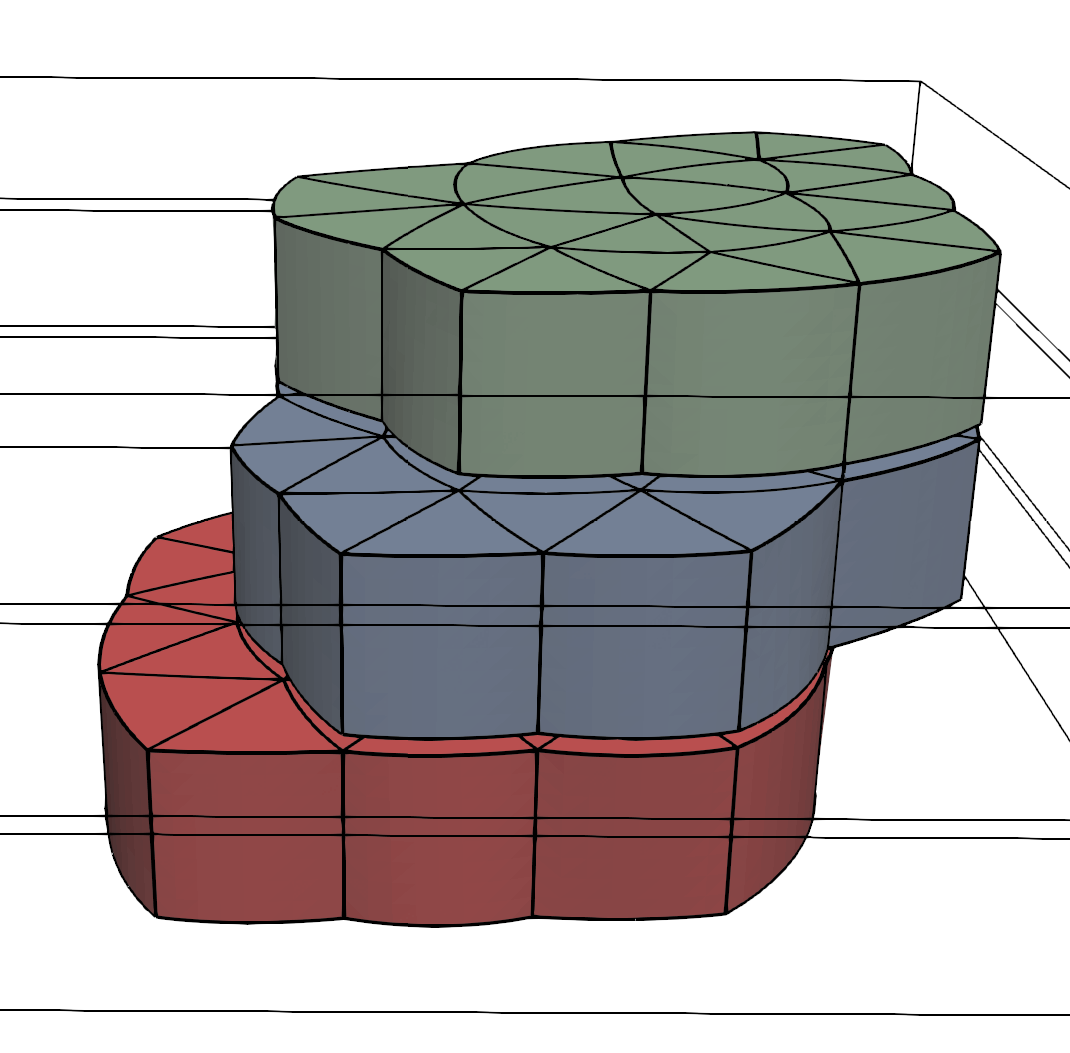
[HLS25]
|
Martin Halla, Christoph Lehrenfeld, and Paul Stocker.
A new T-compatibility condition and its application to the
discretization of the damped time-harmonic Galbrun's equation.
IMA Journal on Numerical Analysis, pages 1--31, 08 2025.
[ bib |
DOI |
arXiv |
http |
.pdf ]
Keywords: discrete approximation schemes, weak T-coercivity, Galbrun’s equation
|
[HL25]

|
Fabian Heimann and Christoph Lehrenfeld.
Geometry error analysis of a parametric mapping for higher order
unfitted space-time methods.
IMA Journal of Numerical Analysis, pages 1--55, 2025.
[ bib |
DOI |
arXiv |
http |
.pdf ]
Keywords: unfitted FEM, space-time, geometry error analysis
|
[LvBV24]
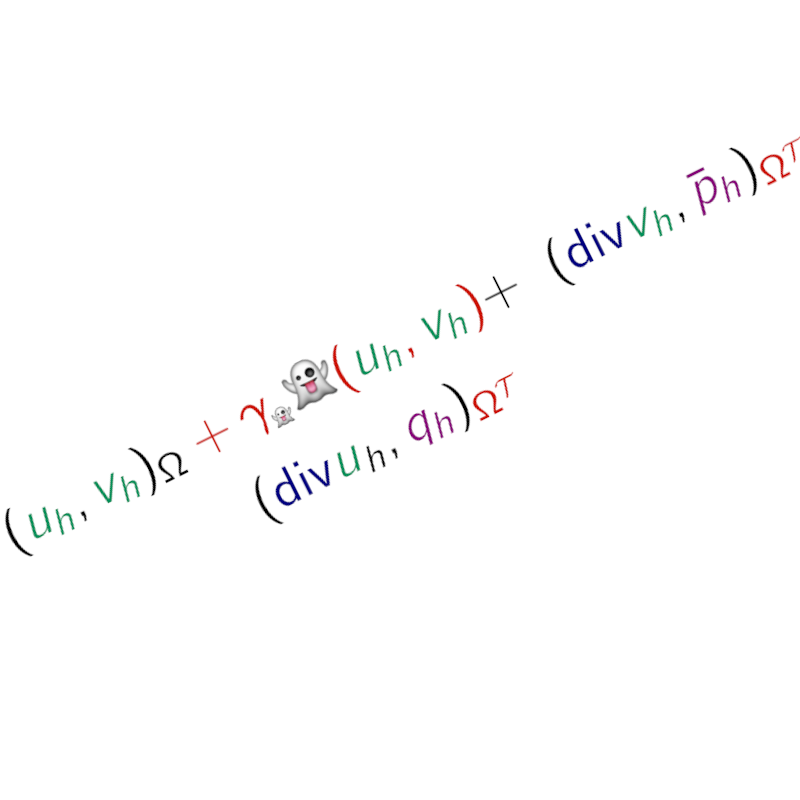
|
Christoph Lehrenfeld, Tim van Beeck, and Igor Voulis.
Analysis of divergence-preserving unfitted finite element methods for
the mixed Poisson problem.
Math. Comp., 2024.
[ bib |
DOI |
arXiv |
code |
http |
http ]
Keywords: unfitted FEM, mixed FEM, divergence-preserving FEM, mixed Poisson problem
|
[LLS24]
|
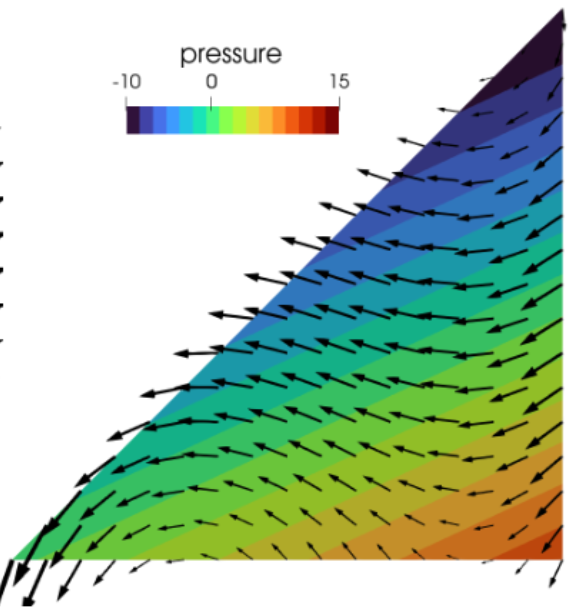
Philip L. Lederer, Christoph Lehrenfeld, and Paul Stocker.
Trefftz Discontinuous Galerkin discretization for the Stokes
problem.
Numerische Mathematik, 2024.
[ bib |
DOI |
arXiv |
code |
.pdf |
.pdf ]
Keywords: Trefftz-DG, Stokes
|
|
[BFG+23]
|
Tobias Boege, René Fritze, Christiane Görgen, Jeroen Hanselman, Dorothea
Iglezakis, Lars Kastner, Thomas Koprucki, Tabea Krause, Christoph Lehrenfeld,
Silvia Polla, Marco Reidelbach, Christian Riedel, Jens Saak, Björn
Schembera, Karsten Tabelow, and Marcus Weber.
Research-Data Management Planning in the German Mathematical
Community.
Eur. Math. Soc. Mag., pages 40--47, 2023.
[ bib |
DOI |
http |
.pdf ]
Keywords: History and Overview (math.HO), FOS: Mathematics, FOS: Mathematics
|
[HLSvW23]
|
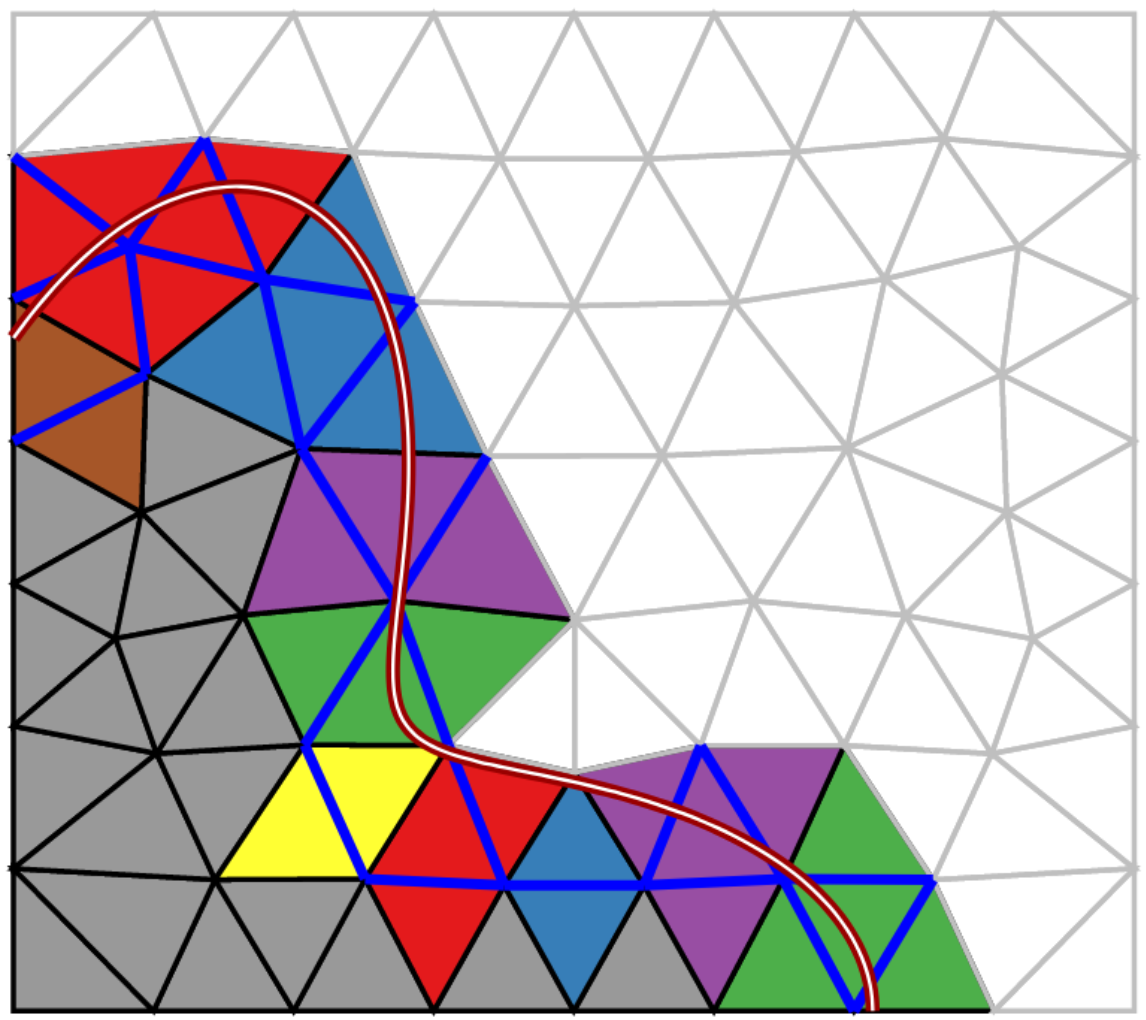
Fabian Heimann, Christoph Lehrenfeld, Paul Stocker, and Henry von Wahl.
Unfitted Trefftz discontinuous Galerkin methods for elliptic
boundary value problems.
ESAIM: M2AN, 57(5):2803--2833, September 2023.
[ bib |
DOI |
video |
code |
http |
.pdf ]
Keywords: Numerical Analysis (math.NA), Unfitted FEM, Trefftz DG, Aggregated FEM
|
[LS23]
|
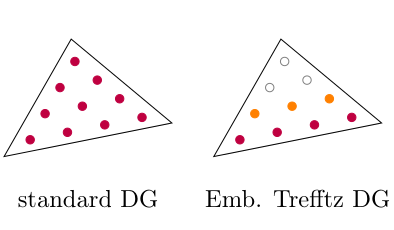
Christoph Lehrenfeld and Paul Stocker.
Embedded Trefftz Discontinuous Galerkin methods.
International Journal for Numerical Methods in Engineering,
124(17):3637--3661, 2023.
[ bib |
DOI |
code |
http |
.pdf ]
Keywords: Trefftz DG methods, Embedded Trefftz DG methods
|
[HLP23]
|
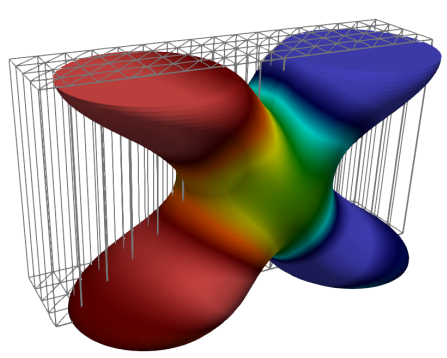
Fabian Heimann, Christoph Lehrenfeld, and Janosch Preuß.
Geometrically Higher Order Unfitted Space-Time Methods for PDEs on
Moving Domains.
SIAM Journal on Scientific Computing, 45(2):B139--B165, 2023.
[ bib |
DOI |
code |
http |
.pdf ]
Keywords: Unfitted FEM, Space-Time FEM, Isoparametric Unfitted FEM, Higher order FEM, Petrov-Galerkin, Galerkin Collocation,
|
[LL22]
|
Yimin Lou and Christoph Lehrenfeld.
Isoparametric unfitted BDF -- finite element method for PDEs on
evolving domains.
SIAM Journal on Numerical Analysis, 60(4):2069--2098, 2022.
[ bib |
DOI |
code |
http |
.pdf ]
Keywords: Eulerian time stepping, isoparametric FEM, unfitted FEM, evolving domains,ghost penalty, stabilization, higher order FEM, BDF, projection errors
|
[Sto22]
|
Paul Stocker.
NGSTrefftz: Add-on to NGSolve for Trefftz methods.
Journal of Open Source Software, 7(71):4135, 2022.
[ bib |
DOI |
code |
http ]
Keywords: numerical software, open source software, NGSolve, Trefftz DG, higher order FEM
|
[HLP21]
|
Thorsten Hohage, Christoph Lehrenfeld, and Janosch Preuß.
Learned infinite elements.
SIAM J. Sci. Comput., 43(5):A3552--A3579, 2021.
[ bib |
DOI |
code ]
Keywords: transparent boundary conditions, Dirichlet-to-Neumann map, helioseismology, learning, infinite elements, rational approximation, Helmholtz equation
|
[LHPvW21]

|
Christoph Lehrenfeld, Fabian Heimann, Janosch Preuß, and Henry von Wahl.
ngsxfem: Add-on to NGSolve for geometrically unfitted
finite element discretizations.
Journal of Open Source Software, 6(64):3237, 2021.
[ bib |
DOI |
code |
http ]
Keywords: numerical software, open source software, NGSolve, unfitted FEM, level set geometries, space-time, higher order FEM
|
[vWRL21]
|
Henry von Wahl, Thomas Richter, and Christoph Lehrenfeld.
An unfitted Eulerian finite element method for the time-dependent
Stokes problem on moving domains.
IMA Journal of Numerical Analysis, 07 2021.
[ bib |
DOI |
arXiv |
code |
http |
.pdf ]
|
[FLLS21]
|
Guosheng Fu, Christoph Lehrenfeld, Alexander Linke, and Timo Streckenbach.
Locking free and gradient robust H(div)-conforming HDG methods
for linear elasticity.
Journal of Scientific Computing, (39), 2021.
[ bib |
DOI |
arXiv |
http |
.pdf ]
Keywords: linear elasticity, nearly incompressible, locking phenomenon, volumelocking, gradient-robustness, Discontinuous Galerkin, H(div)-conforming HDG methods
|
[PHL20]
|
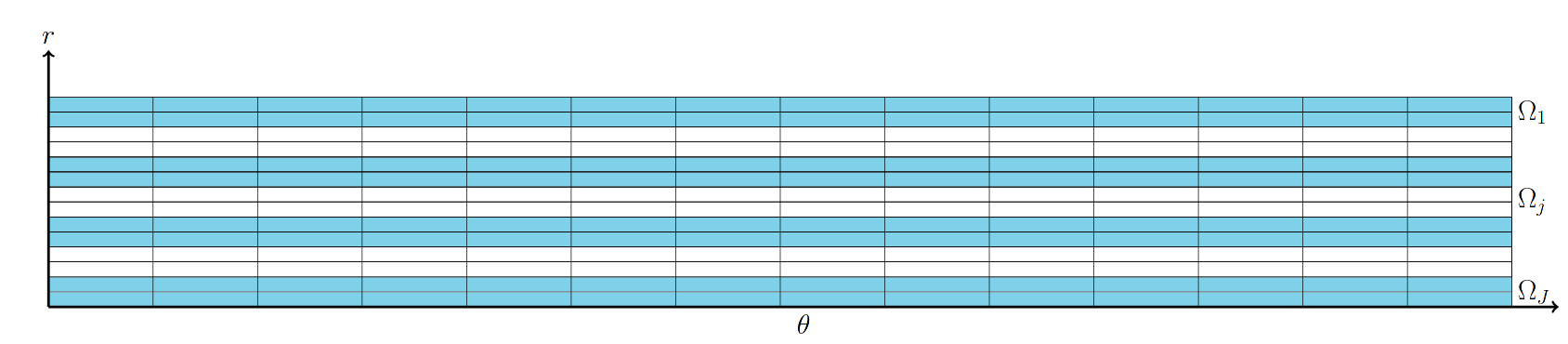
Janosch Preuß, Thorsten Hohage, and Christoph Lehrenfeld.
Sweeping preconditioners for stratified media in the presence of
reflections.
Springer Nature Partial Differential Equations and
Applications, 1, 2020.
[ bib |
DOI |
arXiv |
code |
http |
.pdf ]
Keywords: Helmholtz equation, Dirichlet-to-Neumann operator, Preconditioning, Domain decomposition, High-frequency waves, Computational seismology, Perfectly matched layers, Sweeping preconditioner
|
[LLS20]

|
Philip L. Lederer, Christoph Lehrenfeld, and Joachim Schöberl.
Divergence-free tangential finite element methods for incompressible
flows on surfaces.
121(11):2503--2533, 2020.
[ bib |
DOI |
arXiv |
code |
http |
http ]
Keywords: divergence-conforming finite elements, incompressible Navier-Stokes equations, Piola transformation, surface PDEs, tangential vector field
|
[FKL+19]
|
Niklas Fehn, Martin Kronbichler, Christoph Lehrenfeld, Gert Lube, and
Philipp W. Schroeder.
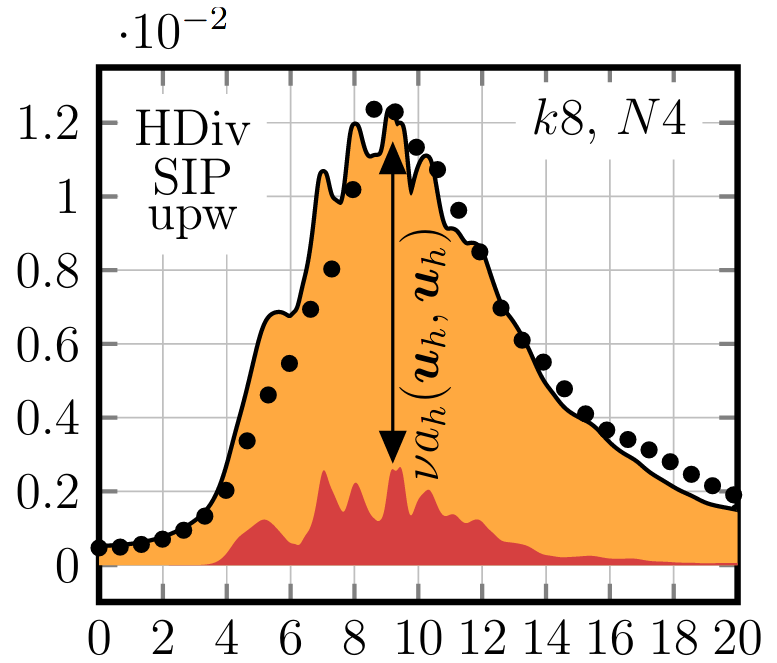
High-order DG solvers for under-resolved turbulent incompressible
flows: A comparison of L2 and H(div) methods.
International Journal for Numerical Methods in Fluids,
91(11):533--556, 2019.
[ bib |
DOI |
http |
.pdf ]
Keywords: discontinuous Galerkin, high-order finite elements, incompressible Navier-Stokes equations, Taylor-Green vortex, turbulent channel flow, underresolved turbulent flows
|
[vWRL+19]
|
Henry von Wahl, Thomas Richter, Christoph Lehrenfeld, Jan Heiland, and Piotr
Minakowski.
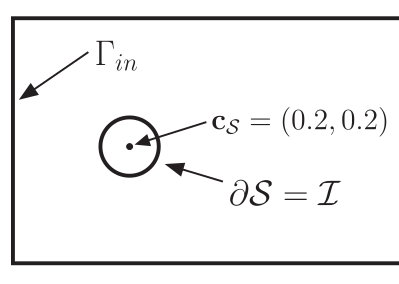
Numerical benchmarking of fluid-rigid body interactions.
Computers & Fluids, page 104290, 2019.
[ bib |
code |
http ]
Keywords: Benchmarking, Computational fluid dynamics, Fluid–structure interaction, Finite elements, Code validation, Reference values
|
[LR18a]
|
Christoph Lehrenfeld and Stephan Rave.
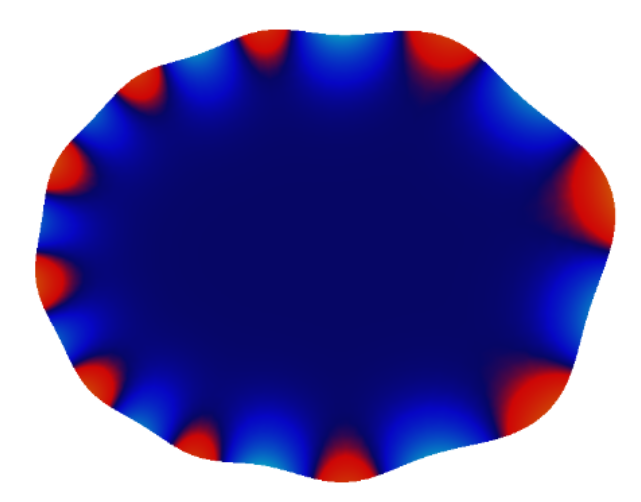
Mass conservative reduced order modeling of a free boundary osmotic
cell swelling problem.
Advances in Computational Mathematics, pages 1--25, 2018.
[ bib |
code |
http |
.pdf ]
|
[LO19]

|
Christoph Lehrenfeld and Maxim A. Olshanskii.
An Eulerian finite element method for PDEs in time-dependent
domains.
ESAIM: M2AN, 53:585--614, 2019.
[ bib |
DOI |
http |
.pdf ]
|
|
[LLS19]
|
Philip L. Lederer, Christoph Lehrenfeld, and Joachim Schöberl.
Hybrid discontinuous Galerkin methods with relaxed
H(div)-conformity for incompressible flows. part ii.
ESAIM: M2AN, 53:503--522, 2019.
[ bib |
DOI |
http |
.pdf ]
|
[SJL+19]

|
Philipp W. Schroeder, Volker John, Philip L. Lederer, Christoph Lehrenfeld,
Gert Lube, and Joachim Schöberl.
On reference solutions and the sensitivity of the 2D
Kelvin--Helmholtz instability problem.
Computers & Mathematics with Applications, 77(4):1010--1028,
2019.
[ bib |
video ]
|
[LOX18]
|
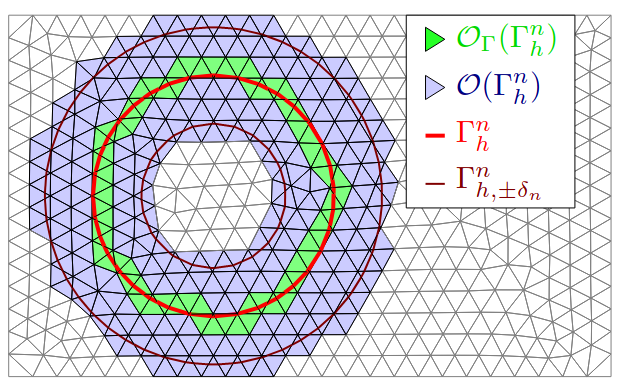
Christoph Lehrenfeld, Maxim A. Olshanskii, and Xianmin Xu.
A stabilized trace finite element method for partial differential
equations on evolving surfaces.
SIAM J. Numer. Anal., 56:1643--1672, 2018.
[ bib |
DOI |
http |
.pdf ]
|
[LLS18]
|
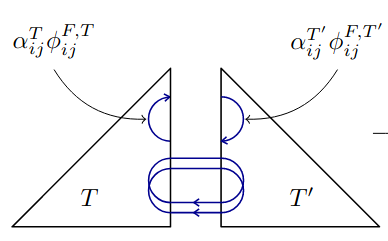
Philip L. Lederer, Christoph Lehrenfeld, and Joachim Schöberl.
Hybrid discontinuous Galerkin methods with relaxed
H(div)-conformity for incompressible flows. part i.
SIAM J. Numer. Anal., 56:2070--2094, 2018.
[ bib |
DOI |
http |
.pdf ]
|
[dPLM18]
|
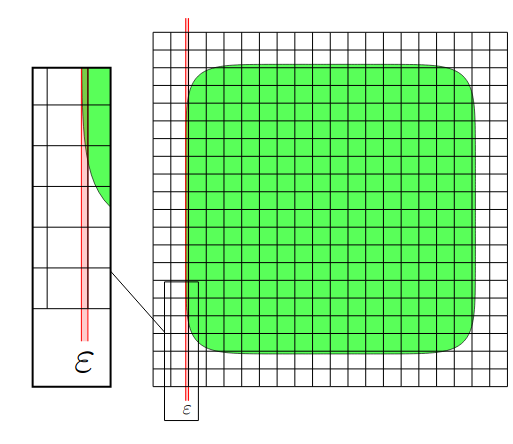
Frits de Prenter, Christoph Lehrenfeld, and André Massing.
A note on the penalty parameter in Nitsche's method for unfitted
boundary value problems.
Computers and Mathematics with Applications, 75:4322--4336,
2018.
[ bib |
DOI |
http |
.pdf ]
|
[SLLL18]
|
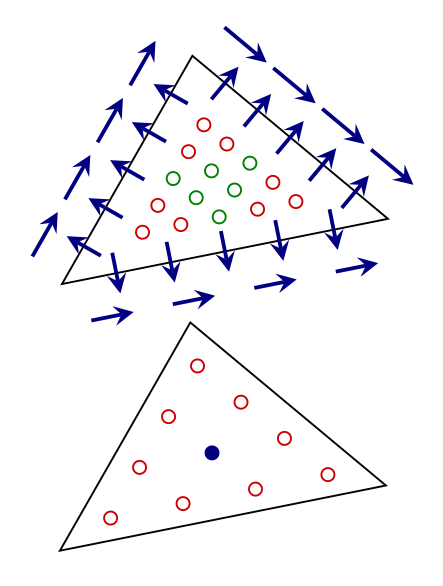
Philipp W. Schroeder, Alexander Linke, Christoph Lehrenfeld, and Gert Lube.
Towards computable flows and robust estimates for inf-sup stable
FEM applied to the time-dependent incompressible Navier-Stokes equations.
SeMA Journal, 75(4):629--653, April 2018.
[ bib |
DOI |
http ]
|
[FL]
|
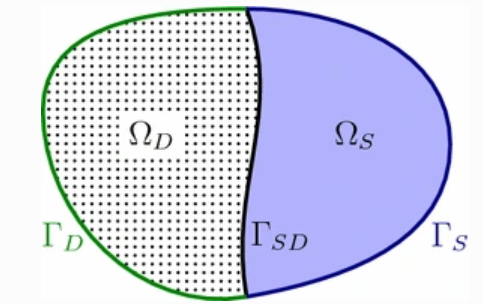
Guosheng Fu and Christoph Lehrenfeld.
A strongly conservative hybrid DG/mixed FEM for the coupling of
Stokes and Darcy flow.
Journal of Scientific Computing, 77:1605--1620.
[ bib |
DOI |
http ]
|
[LR18c]
|
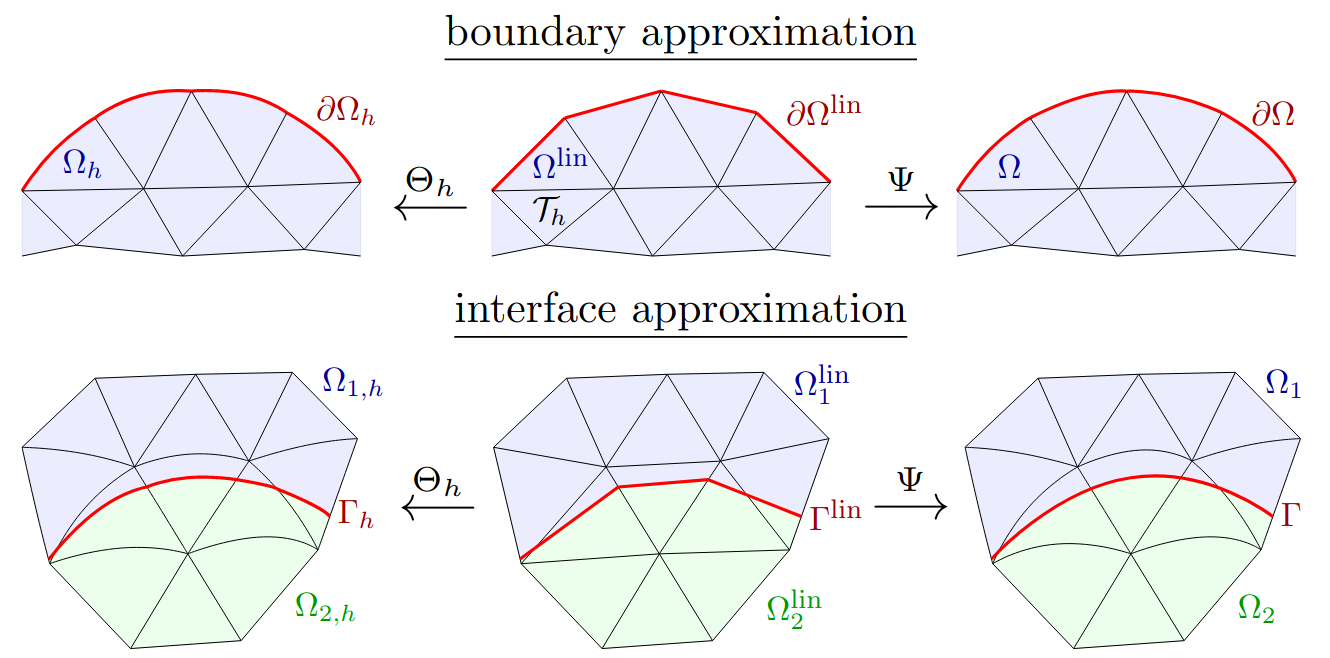
Christoph Lehrenfeld and Arnold Reusken.
L2-estimates for a high order unfitted finite element method for
elliptic interface problems.
Journal of Numerical Mathematics, 00:--, 2018.
first online.
[ bib |
DOI |
http |
.pdf ]
|
[GLR18]

|
Jörg Grande, Christoph Lehrenfeld, and Arnold Reusken.
Analysis of a high-order trace finite element method for PDEs on
level set surfaces.
SIAM Journal on Numerical Analysis, 56(1):228--255, 2018.
[ bib |
http |
.pdf ]
|
|
[LR18b]
|
Christoph Lehrenfeld and Arnold Reusken.
Analysis of a high order unfitted finite element method for an
elliptic interface problem.
IMA J. Numer. Anal., 38:1351--1387, 2018.
[ bib |
DOI |
http |
.pdf ]
|
[LR17]
|
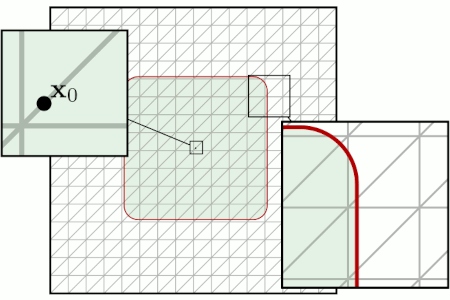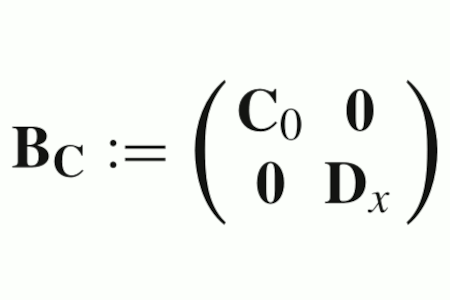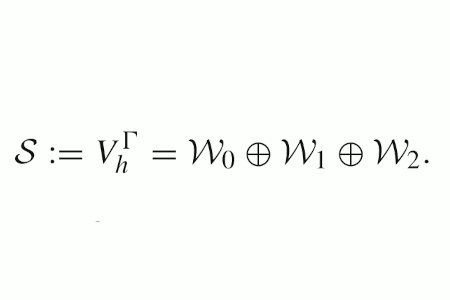
Christoph Lehrenfeld and Arnold Reusken.
Optimal preconditioners for Nitsche-XFEM discretizations of
interface problems.
Numerische Mathematik, 135:313--332, 2017.
[ bib ]
|
[LS16]
|
Christoph Lehrenfeld and Joachim Schöberl.
High order exactly divergence-free hybrid discontinuous Galerkin
methods for unsteady incompressible flows.
Computer Methods in Applied Mechanics and Engineering, 307:339
-- 361, 2016.
[ bib |
DOI |
http |
.pdf ]
|
[Leh16]
|
Christoph Lehrenfeld.
High order unfitted finite element methods on level set domains using
isoparametric mappings.
Computer Methods in Applied Mechanics and Engineering, 300:716
-- 733, 2016.
[ bib |
DOI |
http |
.pdf ]
|
[DLM+16]

|
Carlos J. Falconi D., Christoph Lehrenfeld, Holger Marschall, Christoph Meyer,
R. Abiev, Dieter Bothe, Arnold Reusken, Michael Schlüter, and Martin
Wörner.
Numerical and experimental analysis of local flow phenomena in
laminar Taylor flow in a square mini-channel.
Physics of Fluids, 28(1), 2016.
[ bib |
DOI |
http ]
|
[Leh15]
|
Christoph Lehrenfeld.
The Nitsche XFEM-DG space-time method and its implementation in
three space dimensions.
SIAM J. Sci. Comp., 37(1):A245--A270, 2015.
[ bib |
DOI |
http |
.pdf ]
|
|
[MBL+14]
|
Holger Marschall, Stephan Boden, Christoph Lehrenfeld, Carlos J. Falconi D.,
Uwe Hampel, Arnold Reusken, Martin Wörner, and Dieter Bothe.
Validation of interface capturing and tracking techniques with
different surface tension treatments against a Taylor bubble benchmark
problem.
Computers & Fluids, 102:336 -- 352, 2014.
[ bib |
DOI |
http ]
|
[LR13]
|
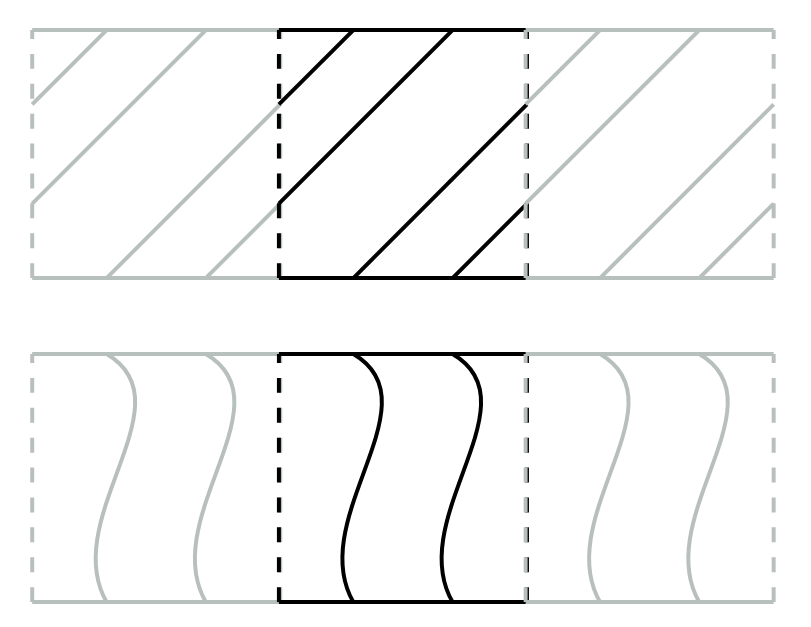
Christoph Lehrenfeld and Arnold Reusken.
Analysis of a Nitsche XFEM-DG discretization for a class of
two-phase mass transport problems.
SIAM J. Numer. Anal., 51:958--983, 2013.
[ bib |
DOI |
http |
.pdf ]
|
[LR12]
|
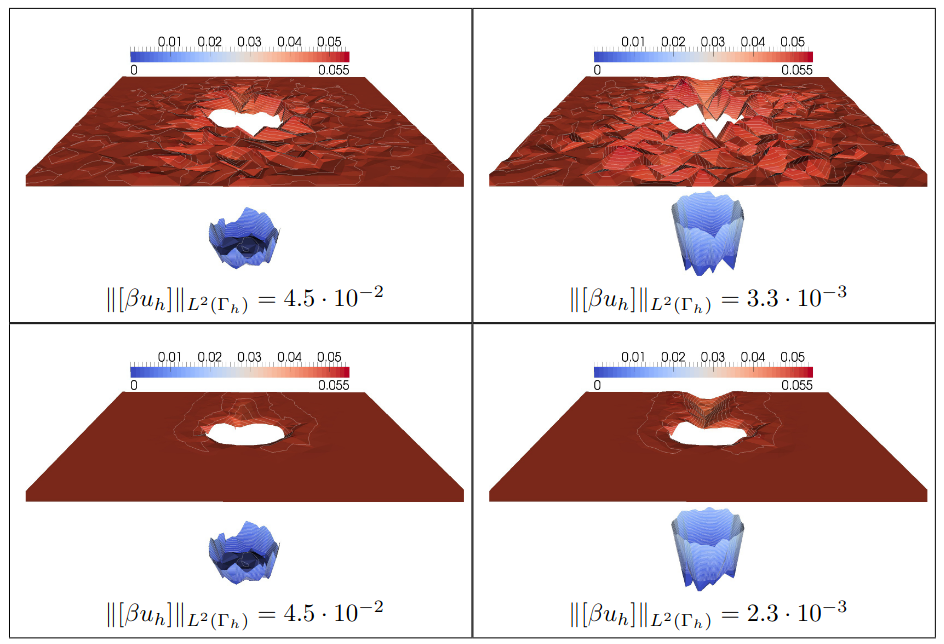
Christoph Lehrenfeld and Arnold Reusken.
Nitsche-XFEM with streamline diffusion stabilization for a
two-phase mass transport problem.
SIAM J. Sci. Comp., 34:2740--2759, 2012.
[ bib |
DOI |
http |
.pdf ]
|
[Rau18]
|
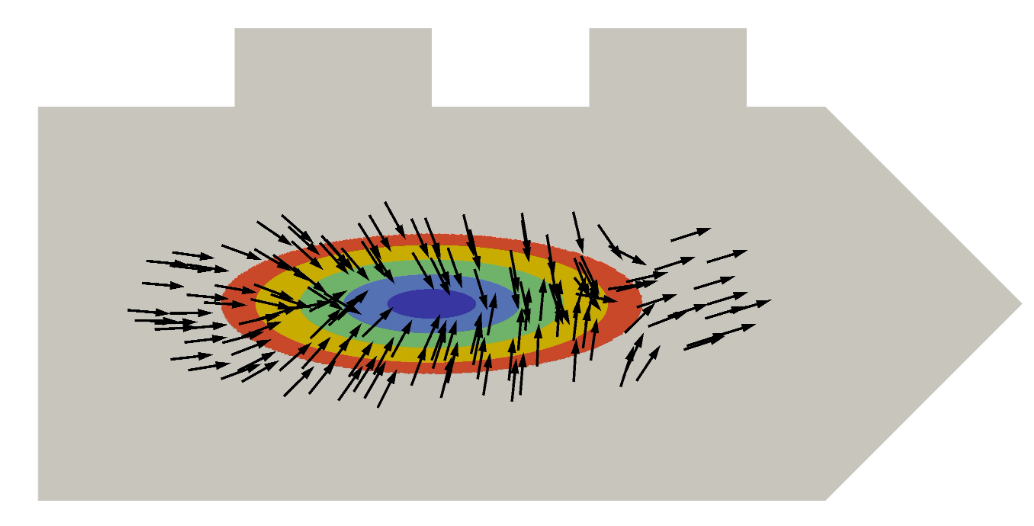
Hans-Georg Raumer.
Shape Optimization for Interface Problems using unfitted Finite
Elements.
Master's thesis, NAM, University of Göttingen, February 2018.
[ bib |
.pdf ]
|
[Pre18]
|
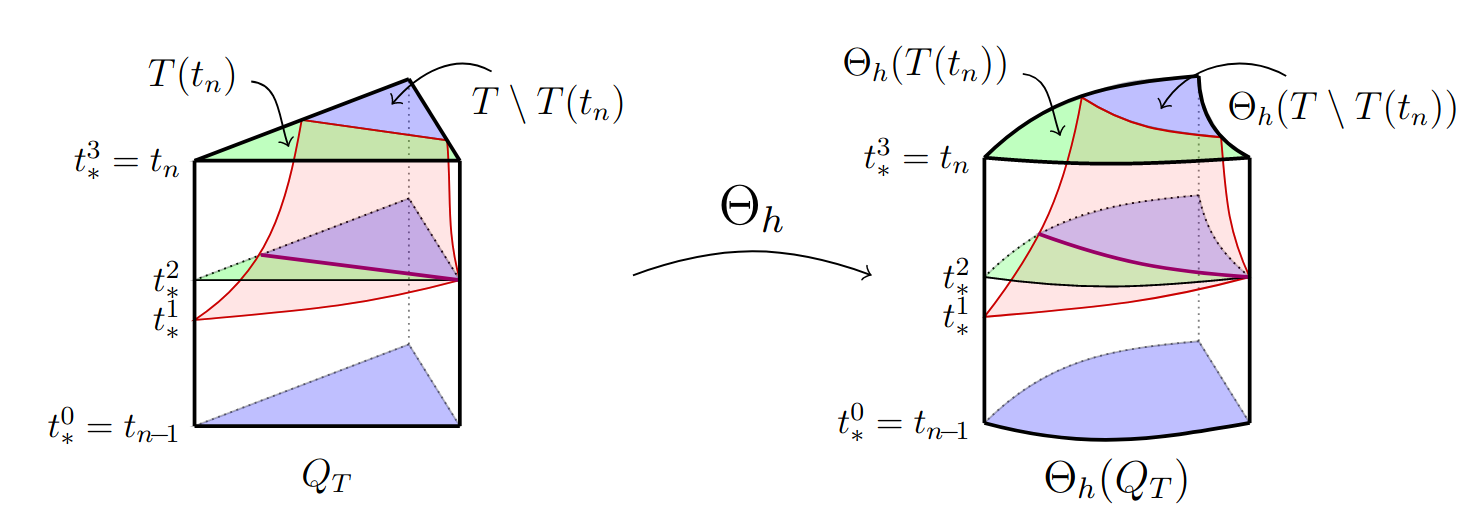
Janosch Preuß.
Higher order unfitted isoparametric space-time FEM on moving
domains.
Master's thesis, NAM, University of Göttingen, February 2018.
[ bib |
DOI |
http ]
|
[Jin19]
|
Xingren Jin.
Higher order stabilized time stepping in unfitted finite element
method on moving domains.
Master's thesis, NAM, University of Göttingen, 2019.
[ bib |
.pdf ]
|
[Hei20]
|
Fabian Heimann.
On Discontinuous- and Continuous-In-Time Unfitted Space-Time Methods
for PDEs on Moving Domains.
Master's thesis, NAM, University of Göttingen, October 2020.
[ bib |
DOI |
http ]
|
|
[Ibr21]
|
Abdul Qadir Ibrahim.
Boundary layer enriched Hybrid Discontinuous Galerkin Methods for
Convection dominated flow.
Master's thesis, NAM, University of Göttingen, June 2021.
[ bib ]
|
|
[Sch21]
|
Anton Schmid.
An HDG method for the Spalart-Allmaras model.
Master's thesis, NAM, University of Göttingen, November 2021.
[ bib ]
|
[Kem22]
|
Michelle Kemper.
Pure Eulerian unfitted FEM for Biological Fluid-Structure
Interaction Problems.
Master's thesis, NAM, University of Göttingen, February 2022.
[ bib |
DOI |
http ]
|
[Rai22]
|
Parajal Rai.
Model Order Reduction for incompressible flows based on structure
preserving discretizations.
Master's thesis, NAM, University of Göttingen, February 2022.
[ bib |
DOI |
code |
http ]
|
[Wen22]
|
Anna Clara Wendler.
Monolithic Unfitted Space-Time FEM for an Osmotic Cell Swelling
Problem.
Master's thesis, NAM, University of Göttingen, February 2022.
[ bib |
DOI |
code |
http ]
|
[Ale22]
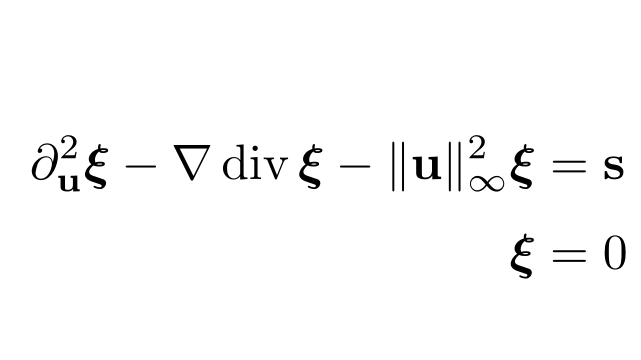
|
Tilman Alemán.
Robust Finite Element Discretizations for a PDE arising in
Helioseismology.
Master's thesis, NAM, University of Göttingen, March 2022.
[ bib |
DOI |
code |
http ]
|
[Kol23]
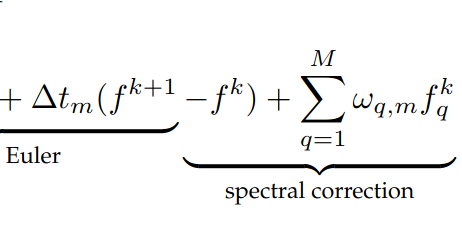
|
Dilini Bhagya Vishwabhakthi Kolombage.
Spectral Deferred Correction Methods for Spatially Discretized Flow
Problems.
Master's thesis, NAM, University of Göttingen, January 2023.
[ bib |
DOI |
code |
http ]
|
[Sch23]
|
Erik Schlesinger.
Embedded Trefftz Trace DG Methods for PDEs on unfitted Surfaces.
Master's thesis, NAM, University of Göttingen, April 2023.
[ bib |
DOI |
video |
code |
http ]
|
|
[Hei24]
|
Constanze Heil.
Space-time Trefftz DG methods for parabolic PDEs.
Master's thesis, NAM, University of Göttingen, March 2024.
[ bib |
DOI |
code |
http ]
|
[van23]
|
Tim van Beeck.
On stable discontinuous Galerkin discretizations for Galbrun's
equation.
Master's thesis, NAM, University of Göttingen, December 2023.
[ bib |
DOI |
code |
http ]
|
[Mey25]

|
Johann Carl Meyer.
On the Conforming Trefftz Finite Element Method and Applications.
Master's thesis, NAM, University of Göttingen, October 2025.
[ bib |
DOI |
code |
http ]
|
[Leh10]
|
Christoph Lehrenfeld.
Hybrid Discontinuous Galerkin Methods for Incompressible Flow
Problems.
Master's thesis, RWTH Aachen, May 2010.
[ bib |
DOI |
http ]
|