Computational PDEs

Fabian Heimann (former member)

Institut für Numerische und Angewandte Mathematik
Lotzestraße 16-18
D-37083 Göttingen
Room 0.125
email: f.heimann@math.uni-goettingen.de
scholar

From 2016 to 2024, I was a member of the working group on Computational PDEs, before moving to University College London. The following page describes my research as of 2024 before the completion of my PhD dissertation.

My research concerns Unfitted Finite Element Methods and how we can exploit their geometric flexibility for moving domains.

Research

Higher Order Unfitted Space-Time Methods

Output: Preprint, SISC, My Master's thesis. Collaborators: C. Lehrenfeld, J. Preuß.

With the Unfitted Higher Order Space-Time Methods, we solve convection-diffusion problems on moving domains. They allow for a straightforward handling of complex geometries and offer a high flexibility in picking time and space discretisation order. For obtaining a higher order geometry approximation in space and time as well, we apply a time-dependent isoparametric mapping. You can observe below how this mapping curves the mesh in a time-dependent manner.

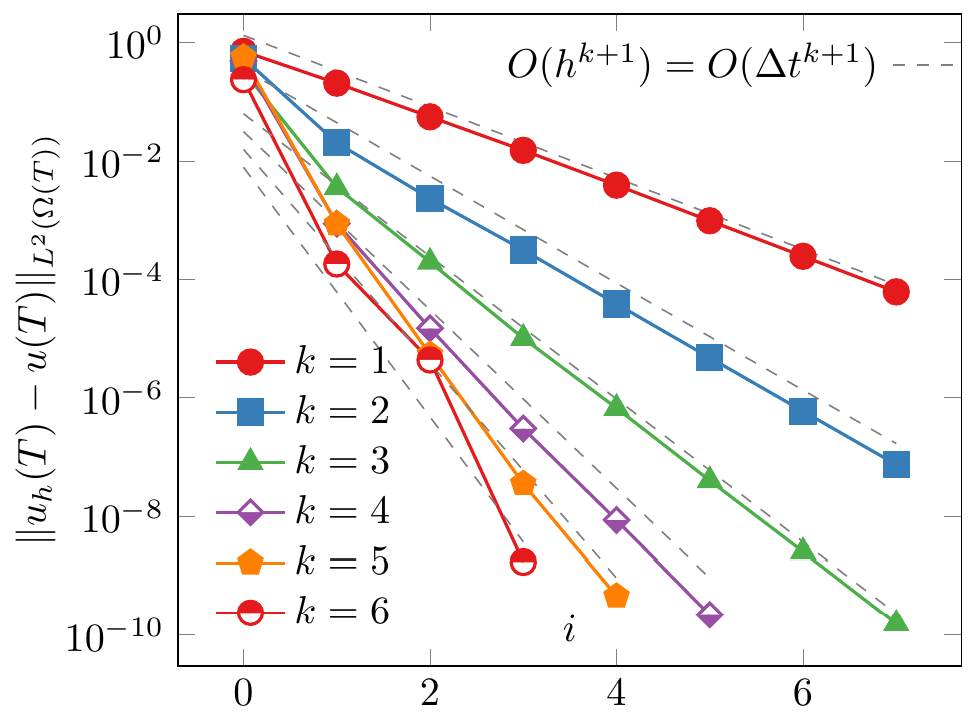
Convergence


Combining these techniques with DG or CG discretisations in time, we are able to observe optimal higher order convergence rates in space and time. The next step is the rigorous mathematical analysis of these properties.

Unfitted FEM for Laplace-Beltrami

Output: My Bachelor's thesis. Collaborators: C. Lehrenfeld, André Massing

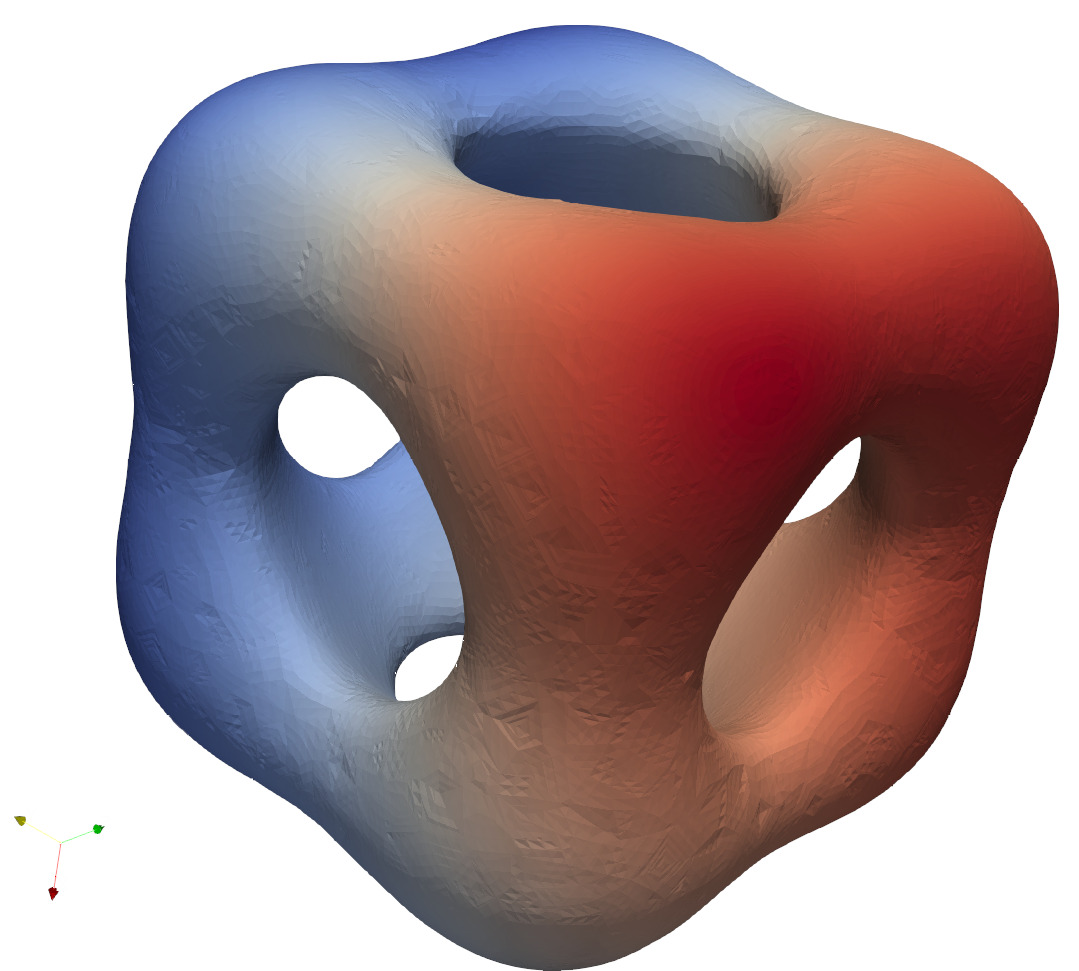
Cheese

The Laplace-Beltrami problem is the surface generalisation of the Poisson/ Laplace equation. We solve it with an Unfitted DG discretisation and ensure higher order convergence by means of the isoparametric mapping. A hybrid DG variant allows for saving computational costs for higher orders.

Unfitted FEM for Soft Tissue

Output: github. Collaborators: ESGI 156 group

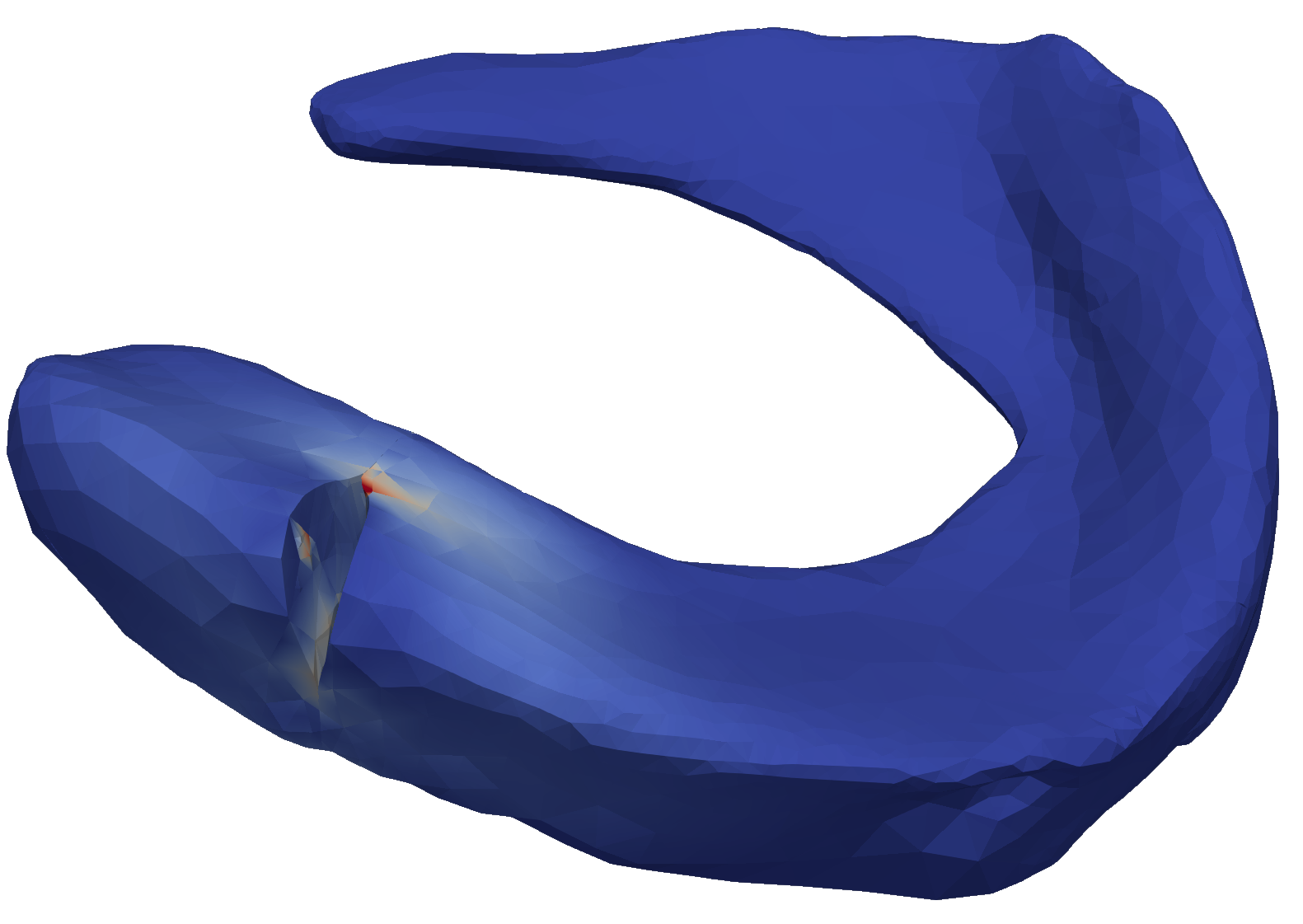
Cheese

At the European Study group with industry 156 in Ålesund, we have been applying the Unfitted Methodology to a Soft Tissue Cutting problem. Within linear elasticity, the discrete displacement function is chosen as the Unfitted combination of discrete polynomials for the left and the right side of the cut. In that way, complex cut shapes can be handled conveniently. We simulate cuts of different depths to arrive at the following animations: Bar, Meniscus.

Implementation of Cut Quadrature Rules

Output: JOSS, Report on Space-Time, ENUMATH 17 Proc

The implementation of Unfitted FE methods (e.g. in our package ngsxfem) requires special routines for integration on cut elements. I have been working on these functions, first specifically for quadrilateral/ hexahedral elements. Later, I have been improving our space-time implementation, so that e.g. simulations in 3 spatial dimensions and time are possible now:

Publications

  • F.H (2024): "A Higher Order Unfitted Space-Time Finite Element Method for Coupled Surface-Bulk problems", arXic preprint, arXiv: 2401.07807, submitted to Proceedings of ENUMATH 2023. Link
  • F.H., Christoph Lehrenfeld (2023): "Geometrically Higher Order Unfitted Space-Time Methods for PDEs on Moving Domains: Geometry Error Analysis", arXiv preprint, arXiv:2311.02348, Nov 2023. Link
  • F.H., Christoph Lehrenfeld, Paul Stocker, Henry von Wahl (2023): "Unfitted Trefftz discontinuous Galerkin methods for elliptic boundary value problems", ESAIM: M2AN 57,2803–2833. Link
  • F.H., Christoph Lehrenfeld, Janosch Preuß (2023): "Geometrically Higher Order Unfitted Space-Time Methods for PDEs on Moving Domains", SIAM Journal on Scientific Computing 45:2, B139-B165. Link.
  • Christoph Lehrenfeld, F.H., Janosch Preuß, Henry von Wahl (2021): "ngsxfem: Add-on to NGSolve for geometrically unfitted finite element discretizations", Journal of Open Source Software, 6(64), 3237. Link.
  • F.H. (2020): "Rabern’s Semantics for Metaphysical and Epistemic Modalities and the Nesting Problem", Journal of Philosophical Logic 49, p. 497–507. Springer Nature. Link.
  • F.H., Christoph Lehrenfeld (2019): "Numerical Integration on Hyperrectangles in Isoparametric Unfitted Finite Elements", in: ENUMATH 2017: Numerical Mathematics and Advanced Applications, Lecture Notes in Computational Science and Engineering 126, p. 193-202. Springer, Cham. Link.

Technical report

  • F.H. (2019): "Implementing cut space-time quadrature rules for three dimensions". Report on implementation progress in ngsxfem. Link

Conferences

I have been presenting my work on international conferences, including ENUMATH 23 (Lisbon), CFC 23 (Cannes), SIAM CSE 23 (Amsterdam), GACM 22 (Essen), GAMM 22 (Aachen), ECCOMAS 22 (Oslo), ICOSAHOM 21 (Online/Vienna), ECCOMAS YIC 21 (Online/Valencia).